Zasięg transmisji zasilaniaW instalacjach monitoringu przemysłowego często zachodzi konieczność poprowadzenia długich przewodów do zasilenia urządzenia elektronicznego, np. kamery. Trzeba tu uwzględnić bardzo ważny parametr, jakim jest „spadek napięcia” na przewodzie. Wielu instalatorów nie zdaje sobie sprawy ze skutków przepływu prądu przez przewody zasilające, a problem zasilania jest podstawą przy projektowaniu każdej instalacji CCTV.
|
Producenci sprzętu podają stałą wartość napięcia zasilania danego urządzenia, np. 12 V DC, ale nie informują o zakresie tego napięcia (wartości minimalnej i maksymalnej). Wykonując praktyczne testy, przyjęliśmy założenie, że dla kamery zasilanej 12 V napięcie może spaść do 11 V. Poniżej tej wartości mogą wystąpić zakłócenia albo utrata sygnału wideo. Czyli spadek napięcia na przewodzie między zasilaczem a kamerą może wynieść maksymalnie 1 V. Wiele osób korzysta z gotowych kalkulatorów zasilania, ale nie zna zagadnień teoretyczno-praktycznych. Dlatego postaramy się je przybliżyć w tym artykule.
|
Każdy przewód ma rezystancję (oporność) większą od 0. Kiedy przez przewód o danej rezystancji płynie prąd, zachodzą dwa zjawiska.
|
1. Występuje spadek napięcia zgodnie z prawem Ohma. 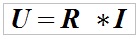
|
2. Energia elektryczna zamieniana jest na ciepło zgodnie z prawem Ohma. 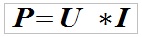
|
albo 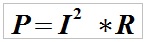
|
Każdy przewód jest rezystorem (opornikiem). Poniżej zamieszono schemat zastępczy przewodu dwużyłowego (uwzględniający tylko rezystancję). 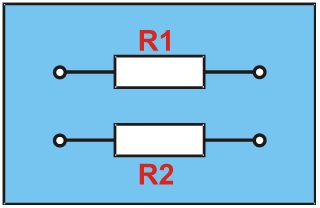
|
Należy uwzględnić spadek napięcia na każdej żyle, dlatego sumaryczna rezystancja (R) przewodu dwużyłowego wyniesie: R = R1 + R2.
|
Poniżej schemat obwodu ilustrujący spadek napięcia w przewodzie dwużyłowym: 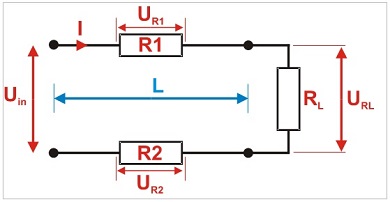
|
gdzie:
Uin – napięcie zasilania, np. z zasilacza,
I – prąd płynący w obwodzie,
R1 – rezystancja (oporność) pierwszej żyły przewodu,
R2 – rezystancja (oporność) drugiej żyły przewodu,
UR1 – spadek napięcia na pierwszej żyle przewodu,
UR2 – spadek napięcia na drugiej żyle przewodu,
L – długość przewodu,
RL – obciążenie, np. kamera,
URL – napięcie na obciążeniu.
|
Po podaniu napięcia z zasilacza (Uin) do przewodu i podłączeniu obciążenia (RL) w układzie zaczyna płynąć prąd (I), powodując spadek napięcia na przewodzie (UR1 + UR2). Zachodzi tu następująca zależność: napięcie wyjściowe na obciążeniu pomniejszone jest o spadek napięcia na przewodzie. 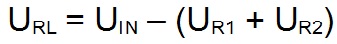
|
Do obliczeń spadku napięcia (Ud) posłużono się poniższym wzorem dla napięcia stałego i zmiennego (1-fazowego): 
|
gdzie:
Ud – spadek napięcia mierzony w voltach (V),
2 – liczba stała, wynikająca z tego, że obliczamy spadek napięcia dla dwóch przewodów,
L – długość przewodu wyrażona w metrach (m),
R – rezystancja (oporność) pojedynczego przewodu wyrażona w omach na kilometr (Ω/km),
I – prąd pobierany przez obciążenie wyrażony w amperach (A).
|
Jak widać, spadek napięcia nie zależy od wielkości napięcia wejściowego, tylko od prądu, długości i rezystancji przewodu.
|
Przeważająca większość kamer przemysłowych ma zmienny pobór prądu. Wynika to z tego, że w nocy załącza się oświetlacz podczerwieni, powodując zwiększenie poboru prądu. Przykładowo kamera w dzień pobiera 150 mA, a w nocy – 600 mA. Nie zaleca się zasilać kamery wyższym napięciem w celu skompensowania straty na przewodzie zasilającym, ponieważ spadek napięcia jest zmienny. Przy długiej linii zasilającej i włączonym oświetlaczu podczerwieni napięcie zasilające kamerę będzie prawidłowe. Wyłączenie się oświetlacza spowoduje zmniejszenie poboru prądu kamery i wzrost napięcia obciążenia, co może skutkować uszkodzeniem kamery.
|
Do obliczeń spadku napięcia potrzebne będą wartości rezystancji pojedynczego przewodu w Ω/km. Sposób obliczeń tych wartości zostanie podany w dalszej części artykułu. W tabelce umieszczono gotowe dane dla kilku przekrojów poprzecznych przewodów.
|
| Przekrój przewodu [mm2] | Rezystancja [Ω/km] (pojedynczy przewód) | | 0,5 | 35,6 | | 0,75 | 23,73 | | 1 | 17,8 | | 1,5 | 11,87 | | 0,19625 (UTP K5 Ø0,5 mm) | 90,7 | | 0,246176 (UTP K6 Ø0,56 mm) | 72,31 |
|
Przykład
Zasilacz 12 V DC, dwużyłowy przewód o przekroju 0,5 mm2 i długości 50 m, kamerę (obciążenie) o poborze prądu 0,5 A (500 mA). Podstawiamy te wartości do wzoru. 
|
Z powyższych obliczeń wynika, że spadek napięcia na tym dwużyłowym przewodzie wyniesie 1,78 V (2 x 0,89 V). Jest to oczywiście suma spadków napięć na poszczególnych żyłach. Czyli napięcie na obciążeniu zmniejszy się do wartości:
12 V – 1,78 V = 10,22 V, co ilustruje poniższy rysunek. 
|
Możemy łatwo obliczyć procentowe straty spadku napięcia na przewodzie zasilającym, korzystając ze wzoru: 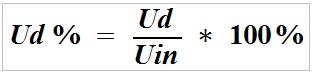
|
gdzie:
Ud% – straty napięcia na przewodzie wyrażone w procentach (%),
Ud – spadek napięcia,
Uin – napięcie wejściowe.
|
Po podstawieniu do wzoru obliczymy zmniejszenie napięcia na obciążeniu w %, czyli straty na linii zasilającej. 
|
Należy zwrócić uwagę, że problem spadku napięcia, zwłaszcza przy niskich napięciach zasilania, jest poważny. Jeżeli zwiększymy napięcie zasilania, to spadek napięcia na przewodzie będzie miał taką samą wartość, ale procentowy spadek napięcia na obciążeniu będzie mniejszy.
|
Przykład
Jak w poprzednim przykładzie: dwużyłowy przewód o przekroju 0,5 mm2 i długości 50 m, kamera (obciążenie) o poborze prądu 0,5 A (500 mA), a także zasilacz 24 V DC. 
|
Straty na linii zasilającej: 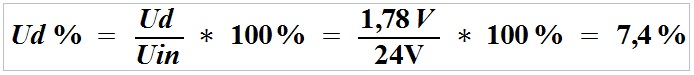
|
Jak widać, spadek napięcia na przewodzie wyniesie 1,78 V, zmniejszając napięcie na obciążeniu z 24 V do 22,22V, czyli o 7,4%, co nie wpłynie na pracę obciążenia.
|
Przykład
Jak w powyższych przykładach: dwużyłowy przewód o przekroju 0,5 mm2 i długości 50 m, kamera (obciążenie) o poborze prądu 0,5 A (500 mA), ale zasilacz 230 V DC. 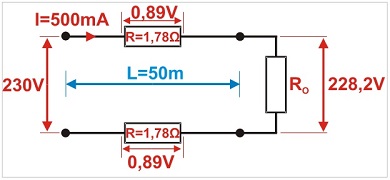
|
Straty na linii zasilającej: 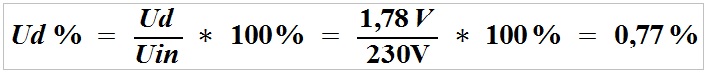
|
Jak widać, spadek napięcia na przewodzie wyniesie 1,78 V, zmniejszając napięcie na obciążeniu z 230 V do 228,2V, czyli o 0,77%, co nie wpłynie na prace obciążenia.
|
Przeanalizowano trzy przypadki zasilania dla różnych napięć. Spadek napięcia jest taki sam i nie wpływa na niego wysokość napięcia zasilającego. O ile w instalacjach 230 V spadek napięcia na obciążeniu o kilka voltów nie ma znaczenia, o tyle przy zasilaniu 12 V problem spadku napięcia może być poważny, powodując nieprawidłowe działanie urządzenia zasilanego.
|
Do powyższych obliczeń potrzebne nam były wartości w Ω/km. Aby samodzielnie obliczyć rezystancję pojedynczego przewodu, musimy poznać tzw. drugie prawo Ohma. Mówi ono, że opór (rezystancja) odcinka przewodu o stałym przekroju poprzecznym jest proporcjonalny do długości tego przewodnika i odwrotnie proporcjonalny do pola powierzchni jego przekroju.
|
Wyraża to wzór do obliczenia rezystancji przewodu o długości L i przekroju S: 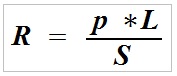
|
gdzie:
R – rezystancja (oporność) pojedynczego przewodu wyrażona w omach (Ω),
p – rezystywność (opór właściwy) przewodu (Ω mm2/m) właściwy dla materiału, z którego wykonano przewód (dla miedzi zawsze podstawiamy wartość 0,0178),
L – długość przewodu wyrażona w metrach (m),
S – pole przekroju poprzecznego przewodnika wyrażone w milimetrach kwadratowych (mm2).
|
Dla miedzi rezystywność wynosi 0,0178 (Ω mm2/m), co oznacza, że 1 m przewodu o przekroju poprzecznym 1 mm2 ma oporność 0,0178 Ω (dla czystej miedzi). Ta wartość jest orientacyjna i może być różna w zależności od czystości i obróbki miedzi. Przykładowo tanie chińskie kable zawierają stopy miedzi z aluminium oraz inne domieszki, co powoduje wzrost rezystywności, a co za tym idzie zwiększa się ich rezystancja i następuje większy spadek napięcia. Dla aluminium rezystywność wynosi 0,0278 (Ω mm2/m).
|
Przykład
Obliczmy opór (rezystancję) przewodu miedzianego o długości 1000 m i o przekroju poprzecznym 0,75 mm2. 
|
Czyli pojedynczy przewód o długości 1000 m ma oporność 23,73 Ω.
|
Znając powyższy wzór i prawo Ohma, bardzo łatwo można obliczyć maksymalny prąd dla konkretnej odległości przewodu o określonym przekroju poprzecznym (w mm2). Do wzoru włączamy cyfrę 2, ponieważ będziemy obliczać realną długość dla 2 przewodów.
|
Przykład
Dysponujemy kablem o długości 30 m i o przekroju 2 x 0,75 mm2.
|
Najpierw obliczmy rezystancję przewodu. 
|
Dla instalacji zasilanej 12 V przyjmujemy spadek napięcia o 1 V. Oznacza to zmniejszenie napięcia na obciążeniu do 11 V. Z prawa Ohma obliczamy maksymalny prąd. 
|
Przykład
Skrętka komputerowa posiada 4 pary przewodów. Obliczmy spadek napięcia przesyłanego 1 parą przy prądzie pobieranym przez obciążenie 500 mA (0,5 A) i długości 40 m dla skrętki UTP K5, która posiada przekrój poprzeczny 0,19625 mm2, zasilanie 12 V.
|
Najpierw obliczmy rezystancję przewodu (skrętka UTP K5 posiada przekrój poprzeczny 0,19625 mm2): 
|
Z prawa Ohma obliczamy sumaryczny spadek napięcia na 2 żyłach dla prądu 500 mA (0,5 A). 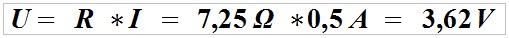
|
Czyli spadek napięcia na linii zasilającej wyniesie 3,62 V, a napięcie przy odbiorniku wyniesie 8,38 V (12 V – 3,62 V = 8,38 V).
|
Możemy też obliczyć z prawa Ohma maksymalny prąd dla spadku napięcia o 1 V dla instalacji zasilanej 12 V, co oznacza zmniejszenie napięcia na obciążeniu do 11 V. 
|
Obliczenia dotyczyły 1 pary skrętki komputerowej. Bardzo często, by zmniejszyć spadek napięcia, wykorzystuje się do przesyłu zasilania 2, 3 lub 4 pary skrętki komputerowej. Łączy się je równolegle, co powoduje zwiększenie się przekroju poprzecznego, a tym samym zmniejszenie rezystancji linii, co wiąże się z mniejszymi stratami napięcia.
|
Gotowe obliczenia dla tych samych parametrów: skrętka UTP K5, prąd 500 mA (0,5 A) i długość 30 m, zasilanie 12 V, to: 1 para – napięcie na obciążeniu = 8,38 V,2 pary – napięcie na obciążeniu = 10,16 V,3 pary – napięcie na obciążeniu = 10,8 V,4 pary – napięcie na obciążeniu = 11,1 V.
|
W poniższej tabeli przedstawiono maksymalny prąd, jaki można przesłać przez przewód o określonej długości i przekroju, tak aby spadek napięcia na obciążeniu nie przekroczył 1 V. Obliczenia wykonano dla 2 żył. | Długość przewodu [m] | Maksymalny prąd – przewód miedziany 2 x 0,5 mm2 [A] | Maksymalny prąd – przewód miedziany 2 x 0,75 mm2 [A] | Maksymalny prąd – przewód miedziany 2 x 1 mm2 [A] | Maksymalny prąd – przewód miedziany 2 x 1,5 mm2 [A] | Maksymalny prąd – przewód miedziany 2 x 2,5 mm2 [A] | | 10 | 1,40 | 2,10 | 2,80 | 4,21 | 7,02 | | 20 | 0,70 | 1,05 | 1,40 | 2,10 | 3,51 | | 30 | 0,46 | 0,70 | 0,93 | 1,40 | 2,34 | | 40 | 0,35 | 0,52 | 0,70 | 1,05 | 1,75 | | 50 | 0,28 | 0,42 | 0,56 | 0,84 | 1,40 | | 60 | 0,23 | 0,35 | 0,46 | 0,70 | 1,17 | | 70 | 0,20 | 0,30 | 0,40 | 0,60 | 1,00 | | 80 | 0,17 | 0,26 | 0,35 | 0,52 | 0,87 | | 90 | 0,15 | 0,23 | 0,31 | 0,46 | 0,78 | | 100 | 0,14 | 0,21 | 0,28 | 0,42 | 0,70 | | 110 | 0,12 | 0,19 | 0,25 | 0,38 | 0,63 | | 120 | 0,11 | 0,17 | 0,23 | 0,35 | 0,58 | | 130 | 0,10 | 0,16 | 0,21 | 0,32 | 0,54 | | 140 | 0,10 | 0,15 | 0,20 | 0,30 | 0,50 | | 150 | 0,09 | 0,14 | 0,18 | 0,28 | 0,46 |
|
Następna tabela przedstawia maksymalny prąd, jaki można przesłać przez skrętkę komputerową o określonej długości, aby spadek napięcia na obciążeniu nie przekroczył 1 V. Obliczenia wykonano dla przesyłu zasilania 1, 2, 3 i 4 parami skrętki komputerowej dla popularnych kategorii 5 i 6. | Długość przewodu [m] | Maksymalny prąd – skrętka komp. UTP K5 1 para
2 x 0,19625 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K5 2 pary
4 x 0,19625 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K5 3 pary
6 x 0,19625 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K5 4 pary
8 x 0,19625 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K6 1 para
2 x 0,246176 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K6 2 pary
4 x 0,246176 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K6 3 pary
6 x 0,246176 mm2 [A] | Maksymalny prąd – skrętka komp. UTP K6 4 pary
8 x 0,246176 mm2 [A] | | 10 | 0,55 | 1,10 | 1,65 | 2,20 | 0,69 | 1,38 | 2,07 | 2,76 | | 20 | 0,27 | 0,55 | 0,82 | 1,10 | 0,34 | 0,69 | 1,03 | 1,38 | | 30 | 0,18 | 0,36 | 0,55 | 0,73 | 0,23 | 0,46 | 0,69 | 0,92 | | 40 | 0,13 | 0,27 | 0,41 | 0,55 | 0,17 | 0,34 | 0,51 | 0,69 | | 50 | 0,11 | 0,22 | 0,33 | 0,44 | 0,13 | 0,27 | 0,41 | 0,55 | | 60 | 0,09 | 0,18 | 0,27 | 0,36 | 0,11 | 0,23 | 0,34 | 0,46 | | 70 | 0,07 | 0,15 | 0,23 | 0,31 | 0,09 | 0,19 | 0,29 | 0,39 | | 80 | 0,06 | 0,13 | 0,20 | 0,27 | 0,08 | 0,17 | 0,25 | 0,34 | | 90 | 0,06 | 0,12 | 0,18 | 0,24 | 0,07 | 0,15 | 0,23 | 0,30 | | 100 | 0,05 | 0,11 | 0,16 | 0,22 | 0,06 | 0,13 | 0,20 | 0,27 |
|
Do wszystkich powyższych obliczeń jest potrzebna znajomość przekroju poprzecznego przewodu wyrażona w milimetrach kwadratowych. Nie należy tego parametru mylić ze średnicą.
|
Dla grubszych przewodów, np. energetycznych, producenci i dystrybutorzy podają przekrój poprzeczny wyrażony w milimetrach kwadratowych (mm2). Natomiast dla cieńszych przewodów, np. telekomunikacyjnych, informatycznych, podawana jest średnica przewodu w milimetrach (mm) i w tych przypadkach musimy przeliczyć średnicę na przekrój poprzeczny.
|
Poniżej rysunek ilustrujący różnicę między przekrojem a średnicą przewodu: 
|
gdzie:
S – przekrój poprzeczny przewodu wyrażony w milimetrach kwadratowych (mm2),
D – średnica przewodu wyrażona w milimetrach (mm),
r – promień przewodu (połowa średnicy) wyrażony w milimetrach (mm),
L – długość przewodu.
|
Wzór do obliczeń przekroju: 
|
albo 
|
π – liczba pi, stała matematyczna = 3,14
|
Przykład
Skrętka komputerowa UTP kat. 5e. Producent podaje średnicę S = 0,5 mm. Obliczmy przekrój poprzeczny w mm2. 
|
albo 
|
Czyli przewód o średnicy 0,5 mm ma przekrój poprzeczny wynoszący tylko 0,19625 mm2.
|
Główne czynniki wpływające na spadek napięcia: prąd – zależność z prawa Ohma: im większy prąd, tym większy spadek napięcia;średnica albo przekrój poprzeczny przewodu – im cieńszy przewód, tym większy spadek napięcia;długość przewodu – logicznie: im dłuższy przewód, tym większa rezystancja i spadek napięcia;materiał, z którego wykonany jest przewód. Dziś większość przewodów jest wykonana z miedzi, która stanowi dobry przewodnik. Na rynku są dostępne tanie chińskie przewody wyglądające jak miedź, ale wykonane ze stopu zawierającego np. aluminium i magnez. Spotyka się też drut stalowy z cienką powłoką miedzianą. Wszystko to przekłada się na większą rezystancję i zwiększony spadek napięcia.
|
|
 Nowe produkty
Nowe produkty